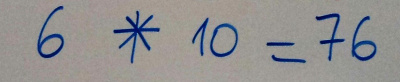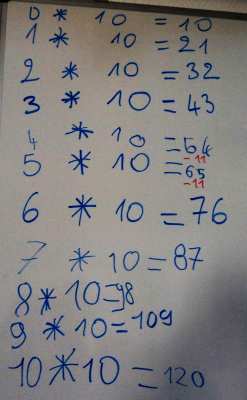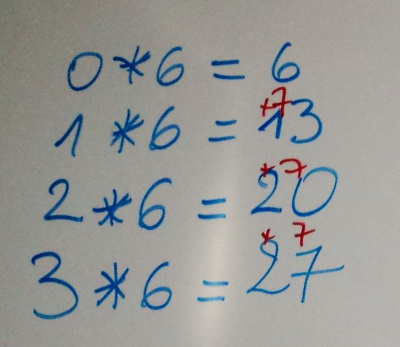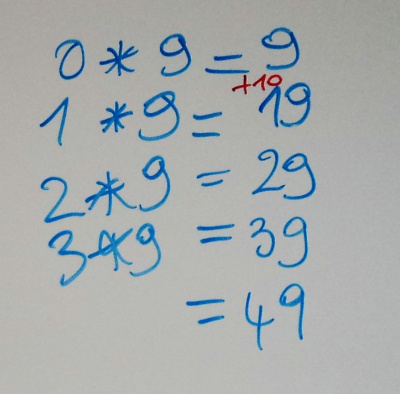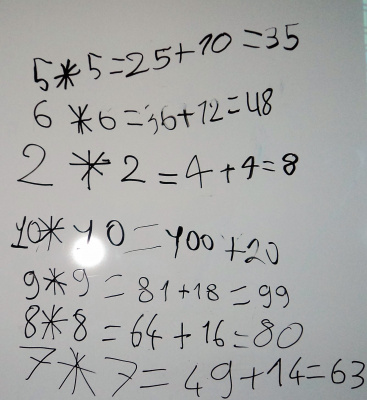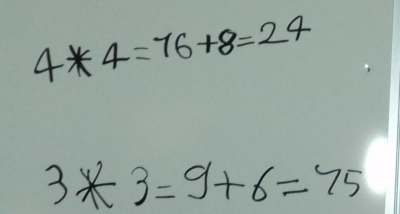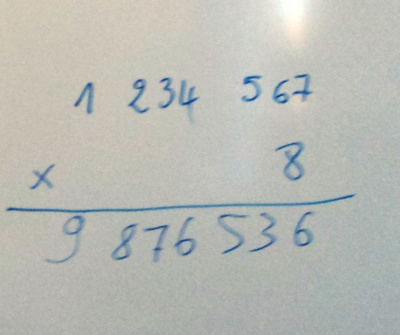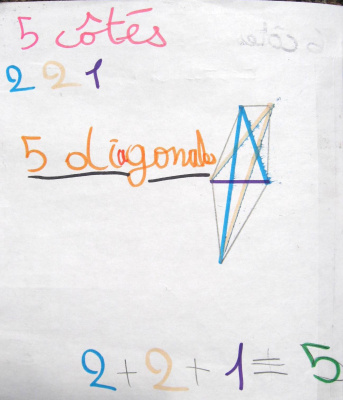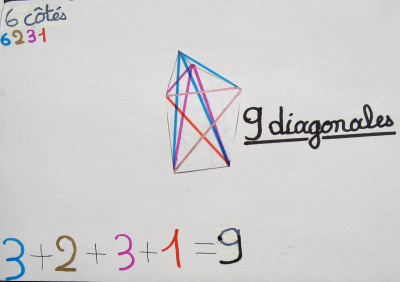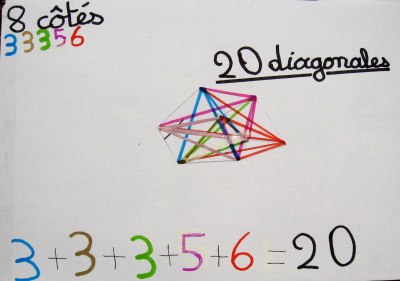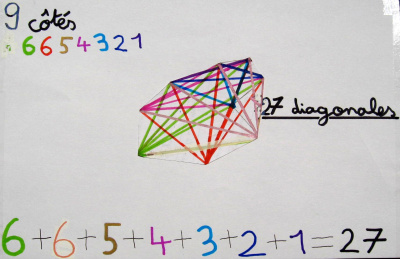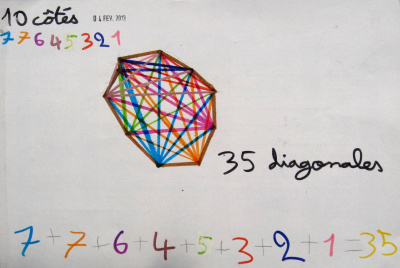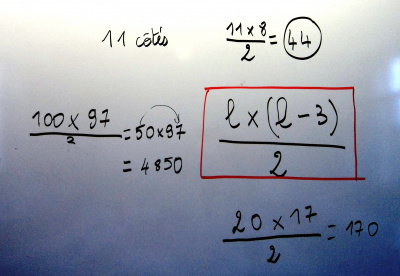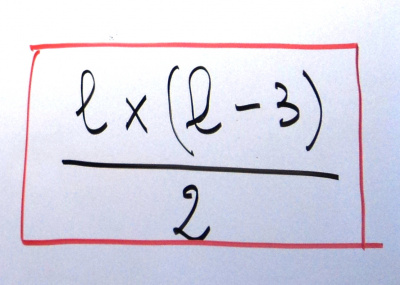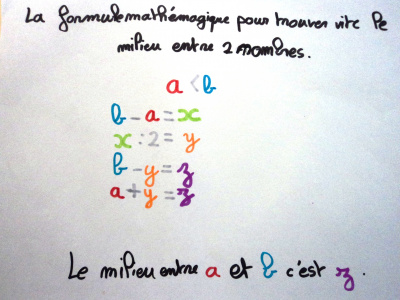Les tables formes d’Emi
Voici une « table » inventée par Emi
Nous avons inventé une opération !
Un jour, Maëlys nous a proposé une création bizarre…
On n’arrivait pas à décider ce que Maëlys avait voulu écrire : un signe + ou un signe x ?
Alors, pour plaisanter, on a proposé que ce soit les deux : ce serait l’opération * (étoile). Mais que faisait-elle, cette opération ?
Facile, a proposé Matis : « d’abord, elle multiplie les nombres entre eux, puis elle ajoute leur somme. Par exemple, ici, voici le résultat : »
6*10, c’est égal à (6 x 10) + (6+10), c’est donc égal à 60 + 16, et donc c’est bien 76 !
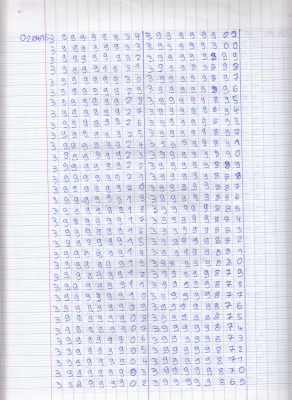
Quelle magnifique proposition ! Nous nous sommes emballés dans la recherche, nous avons alors exploré la table de 10 :
Et bien entendu, nous avons remarqué qu’entre chaque résultat, on ajoutait 11. En effet :
10 + 11 = 21 21 + 11 = 32 32 + 11 = 43
Tiens, tiens, on ajoute 11 à chaque fois et c’est la table de 10… Or 11, c’est 10 +1.
Et pour la table de 6, alors, on ajouterait 7 (qui est égal à 6+1) ? Aussitôt dit, aussitôt testé !
Oui ! ça marche ! Alors là, nous étions vraiment contents et excités. On a testé la table de 9 : si vous avez bien suivi notre raisonnement, on devait ajouter… 10 à chaque fois pour trouver le résultat suivant.
Youpi, ça marchait à nouveau. Inutile de vous décrire notre enthousiasme et notre fierté !
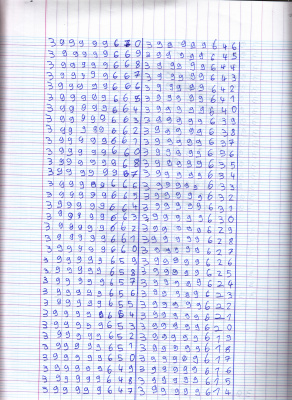
La fois suivante, nous avons exploré méthodiquement la table de l’opération étoile…
Maëlan avait choisi une présentation en colonnes :
Tandis qu’Elzéar et Matis avaient opté pour la présentation en tableau à double entrée, comme Pythagore.
Tous ensemble, au tableau, nous avons commencé à remplir la table en tableau avec l’aide de la table en colonnes, en vérifiant les résultats. Pour cela, nous avons décomposé chaque étape : d’abord on calcule le PRODUIT des 2 nombres (on fait une multiplication) puis la SOMME des deux nombres (on fait une addition).
Nous nous sommes concentrés sur la ligne diagonale de la table.
Voici où nous sommes rendus, mais nous sommes loin d’avoir terminé !
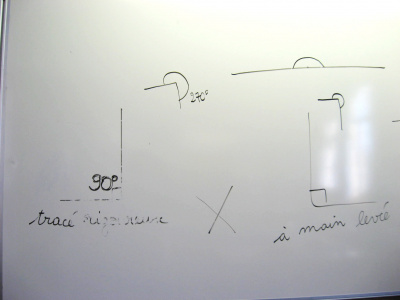
Un cercle tracé avec une règle ?
Un jour, au premier trimestre, quelqu’un a proposé d’essayer de tracer un cercle sans compas, à la règle…
Depuis, il y a eu bien des essais, des propositions…
puis, il a essayé de tracer le cercle,
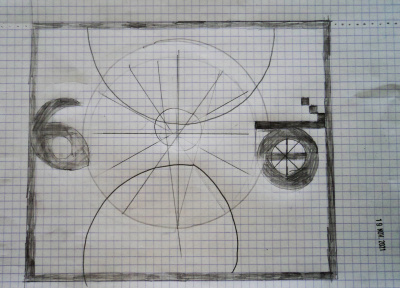
Un jour, Maëlwenn nous a rappelé une recherche qu’elle avait vue affichée dans la classe l’année dernière : ça a donné des idées à Emi, qui a voulu prolonger les réalisations très belles de Lysa et Elia.
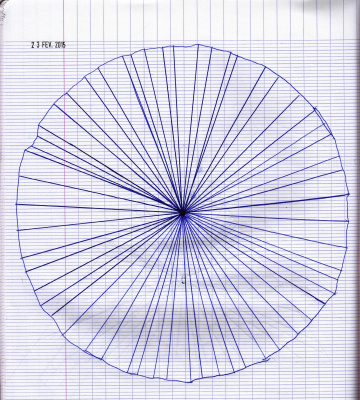
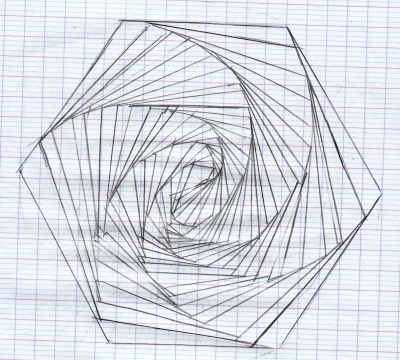
Emi a essayé avec des polygones de plus de 12 côtés :
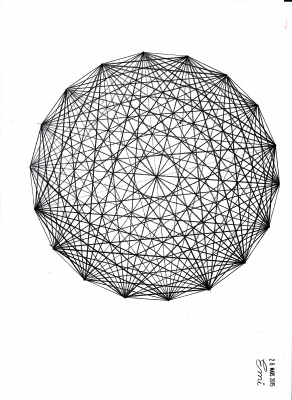
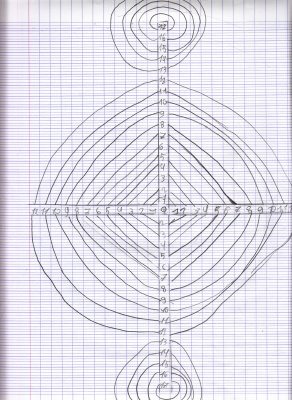
- Le 26 mars, Emi nous présente son travail : elle a tracé toutes les diagonales d’un polygone presque régulier à 18 côtés. Et là, surprise ! Il y a un cercle qui apparaît nettement au milieu.
Et même d’autres cercles remarque Clara… Nous comptons 7 cercles concentriques, de plus en plus difficiles à voir plus on s’éloigne du centre. Par quel mystère ?
Nous ne savons pas y répondre, mais nous faisons des essais pour continuer nos explorations de l’idée de départ : tracer un cercle avec une règle, sans compas.
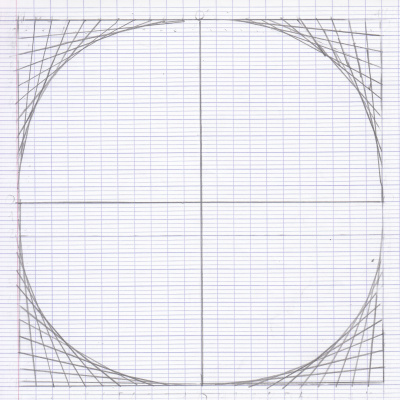
Nous utilisons parfois de très grandes feuilles à petits carreaux (de format A2, c’est-à-dire l’équivalent de 2 feuilles A3 collées).
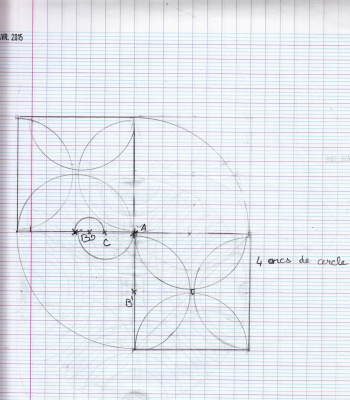
Et même, des arcs de cercles très précis : des quarts de cercle.
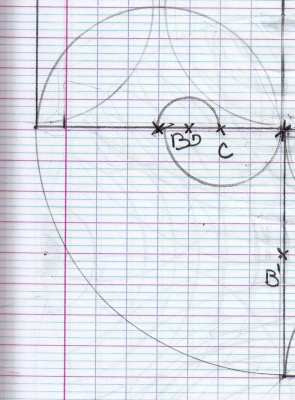
Le 10 avril, Maëlwenn a photocopié son travail 4 fois, pour essayer de faire un grand cercle à partir de son quart de cercle.

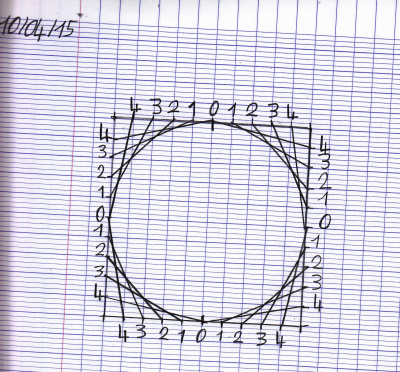
- Chez elle, Maëlwenn a tracé un cercle à la règle dans un carré de 5 cm de côté.
… on a cherché un moyen de coder la trouvaille de Maëlwenn pour que tout le monde puisse la refaire. Voilà notre codage :
- 8 X (0 ;4)
- 8 X (1 ;3)
- 4 X (2 ;2)
Evan, lui, il s’est dit qu’il pourrait essayer autre chose…
Les arcs de cercle de Lisa
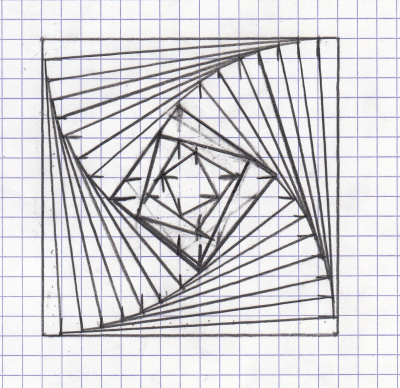
Moya a inscrit des carrés dans des carrés,
et ça a inspiré Youenn.
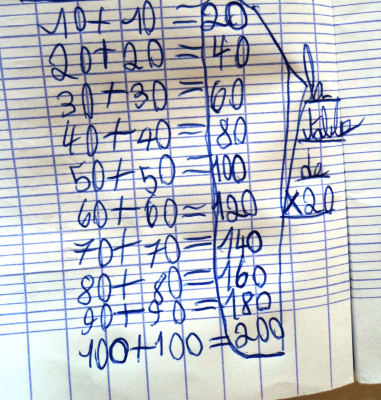
La table de 20 d’Élodie
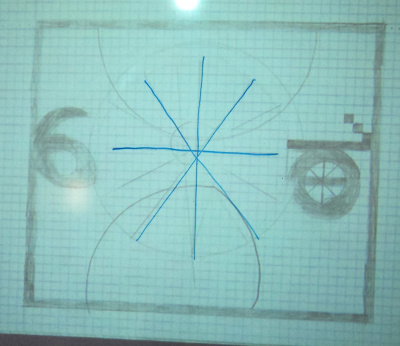
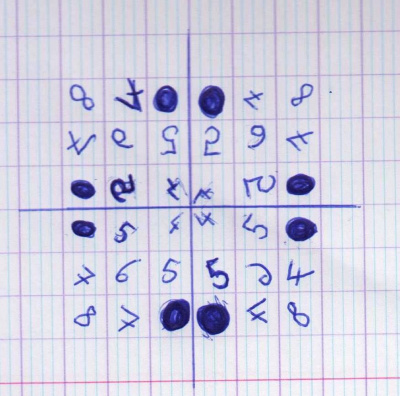
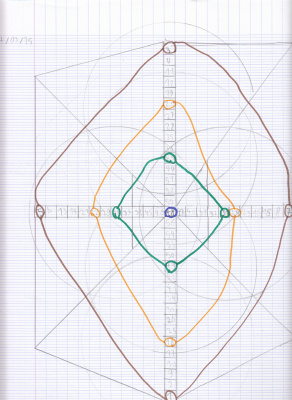
Une création avec des axes de symétrie de Clara
Au tableau, Laël a remarqué qu’il y avait deux axes de symétrie.
On a tracé d’abord un seul axe de symétrie pour nous aider à vérifier chaque chiffre.
Lisa et Laura G ont participé à « redresser » les 7.
Ensuite, quand on a tracé l’autre axe de symétrie, Clara a remarqué que c’était difficile de corriger un seul axe à la fois. Elle a décidé de tout recommencer proprement.
Cette fois, c’est mieux ! a dit Marllay.
Avec quels outils pourrait-on réussir parfaitement le travail que s’est proposé Clara ? On va essayer avec le compas, ou alors du papier calque et une punaise.
Comment pourrait-on définir autrement cette double symétrie ? On dirait que ça tourne… On pense que c’est aussi une rotation !
Des nombres géants… le travail de titan d’Esteban
Un jour, Jasonn s’est proposé de calculer 400 millions moins 1 million, moins 1 million, moins 1 million, … Il l’a présenté au groupe.
Esteban, qui a bien regardé le travail de Jasonn, a proposé de le transformer. Il s’est dit, moi, je vais calculer…
Alors, avez-vous vu l’opération qu’Esteban a calculée ? Et combien de fois l’a-t-il recommencée ?
Les carrés codés de Maélys
Un jour, le groupe de Thomas passait au tableau. Pendant ce temps, Maélys, qui était dans l’autre groupe, regardait et écoutait tout en faisant ses propres essais.
Ce jour-là, dans le cahier de mathématiques de Thomas, nous avons vu ça…
Mais il n’y avait pas encore les couleurs, nous les avons mises ensemble en étudiant son travail au tableau.
On a cherché, tous ensemble, comment Thomas avait fait.
On a découvert qu’il avait mis les nombres deux par deux en commençant par tout en bas, puis tout en haut, puis à gauche, puis à droite.
On a proposé d’autres façons de mettre les nombres.
Maélys, pendant ce temps, sur son cahier jaune, a réalisé ça :
Alors, quand elle l’a présenté au groupe, à son tour, au tableau, on lui a dit que c’était réussi, mais qu’elle pourrait le refaire en plus appliqué…
C’est mieux réussi, a dit Marllay !
Et maintenant, qu’est-ce qu’on pourrait lui dire ?
Quelle sorte de mathématiques est-ce donc ?
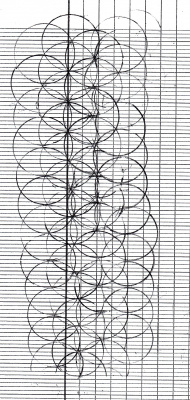
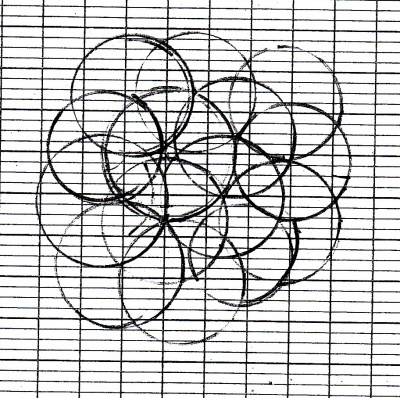
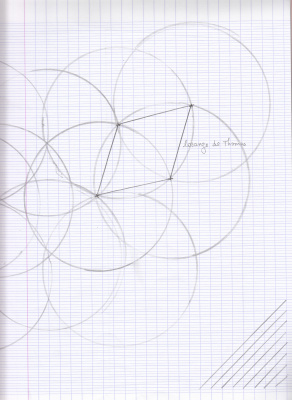
Le pavage de rosaces de Valentin
Ensuite, il a essayé de couvrir toute une surface de rosaces.
Et le plus difficile : sur du papier blanc !
Lors de la projection à la classe, nous avons marqué au feutre tous les centres pour compter le nombre de cercles qu’il avait tracés. Et quand nous avons éteint le vidéoprojecteur, nous avons remarqué que des points étaient alignés.
Ce travail a donné envie à Thomas d’essayer…
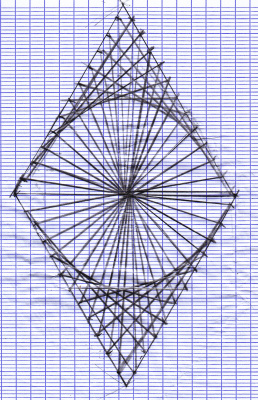
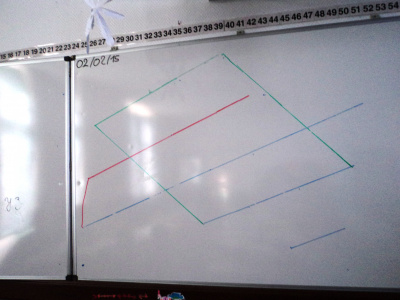
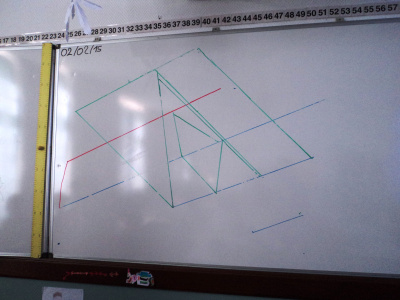
Le losange de Thomas
Mais au bout de 4, on s’est arrêtés, surpris :
Alors, on a tracé le losange. Et Thomas, étonné, a dit : « ah ben moi, je le savais même pas qu’il y avait un losange caché là ! »
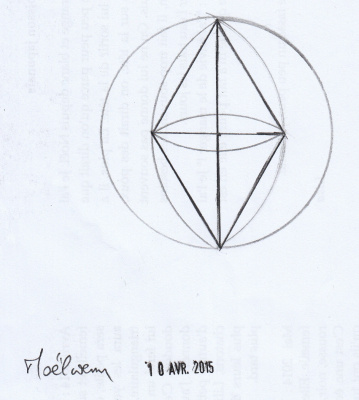
Un peu plus tard, Maëlwenn a essayé une autre technique, proposée par Marllay, pour tracer un losange :
Carla et Hugo, nos correspondants de La Ciotat, nous ont écrit à propos de cet article
Comme notre site ne permet pas d’agrandir les images, nous avons retranscrit leur courrier :
"Bonjour Thomas et Maëlwenn,
Nous sommes Hugo et Carla, élèves de 2de Freinet à La Ciotat et nous avons été interpelés par vos travaux remarquables sur les losanges. Nous aussi avons été étonnés de voir apparaître un losange à partir des centres. Mais nous avons plusieurs questions avant de poursuivre ce travail de recherche avec vous :
1- Thomas, comment as-tu eu l’idée de faire un pavage de rosaces ?
2- As-tu des mesures à indiquer pour tes cercles ou les as-tu faits aléatoirement sur ta feuille ?
3- Comment peux-tu affirmer que c’est un losange ?
4 - Maëlwenn, peux-tu nous donner ton programme de construction ? 5 - A quoi sert l’ovale au centre du losange ?
Nous avons essayé de répondre à ce courrier, en aidant Thomas à formuler quelques réponses à Hugo et Carla :
1- Au début, j’ai voulu envahir ma feuille de cercles. Au bout d’un moment, j’en ai eu assez.
2- Mon copain Marllay m’a aidé à trouver pourquoi c’est un losange. Cette figure a :
- 4 côtés de même longueur
- 4 sommets
- 2 angles aigus
- 2 angles obtus
Des questions sans réponse…
Une question de vocabulaire… En anglais, « numbers » c’est nombre et numéro. Mais en français, On se demande si :
et aussi, pourquoi cette opération a l’air un peu magique :
La pyramide des + de Laura G
Dans notre classe, depuis le début de l’année, on aime bien réaliser des pyramides de toutes sortes. Laura G a décider de fabriquer la pyramide des +.
Laura a défini une règle de calcul, et elle l’applique.
Comme c’est difficile de scanner cette grande feuille, on va vous dire ce qu’elle fait : elle ajoute les nombres des 2 cases à gauche et au-dessus d’une case, et elle écrit le résultat. Mais les nombres sont si grands qu’ils ne rentrent plus dans les cases depuis longtemps !
Alors, elle a inventé des codages avec les couleurs.
Mais à leur tour, les codages avec des couleurs ne rentraient plus. Alors Estelle et Laura G, qui se sont mises ensemble pour réussir ce long travail, ont décidé d’adopter un autre système, avec des lettres et des couleurs.
Mais elles sont fatiguées de ce travail si difficile… Pourtant, elles voudraient bien connaître le plus grand nombre, on a réfléchi ensemble et on sait dans quelle case il sera.
N’auriez-vous pas une technique rapide qui les aide à trouver ce fameux « plus grand nombre de la pyramide des + de Laura G » ?
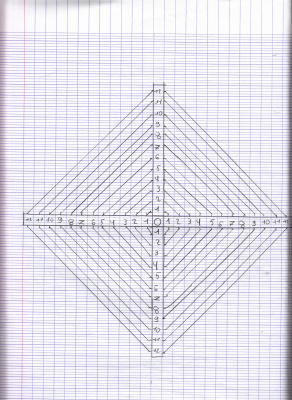
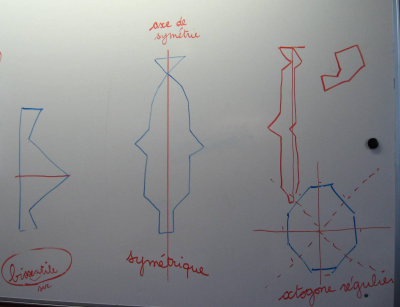
Une symétrie de Zoé
Dans la classe, on a fait beaucoup de figures symétriques, de toutes sortes, des plus simples aux plus compliquées…
Zoé, elle, a choisi de faire une symétrie axiale avec deux axes de symétrie perpendiculaires.
On a vérifié, il n’y en a pas plus que deux.
Par contre, on a vu un carré dans la figure de Zoé. Alors, on a tous fait un carré, et on a cherché combien un carré a d’axes de symétrie…
En le pliant, on est sûrs de notre résultat !
Laël invente avec un tangram

- On a vu une autruche, un paon, un papillon qui sort de son cocon… mais Laël a fait la reine d’Angleterre ! Et si c’était une autruche d’Angleterre vu de derrière, qui se retourne pour nous regarder ? Ou alors le Cyclope Brontès ?
Quelques jours plus tard, Laël offre à la classe une fiche avec des puzzles réalisés avec un tangram, …
et il les réalise.
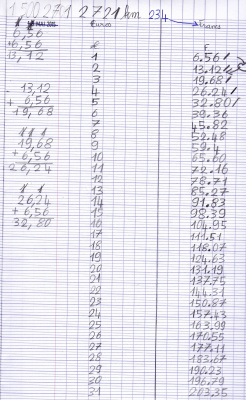
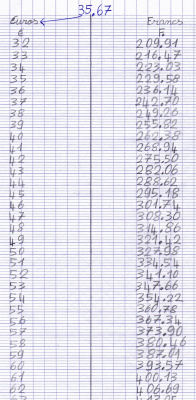
Emi a découvert un convertisseur d’euros
Une discussion s’engage ensuite avec Hugo et Carla, élèves de Seconde.
Avant 2002, on utilisait une monnaie nationale en France : les francs. Et chaque pays européen avait sa monnaie : les pesetas en Espagne, les drachmes en Grèce, les marks en Allemagne… Tous ces pays utilisent l’euro depuis 2002. Lorsqu’on est « passé à l’euro », les gens utilisaient des convertisseurs pour se rendre compte du prix des choses.
Cela a donné envie à Esteban de continuer :
Nos correspondants du lycée Lumière de La Ciotat ont écrit à Emi au sujet de son travail !
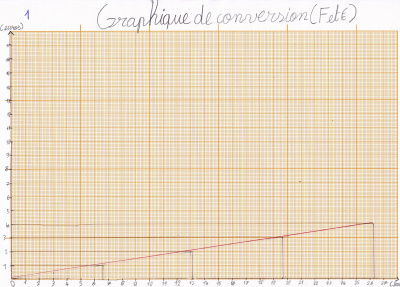
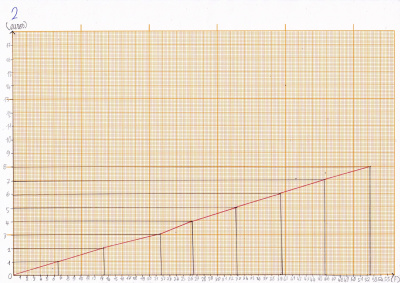
Emi a réalisé deux graphiques en suivant les propositions d’Hugo et Carla.
Le premier n’allait pas bien loin… Alors elle s’est demandé si c’était possible de choisir une échelle différente pour chaque axe, pour « aller un peu plus loin ». Marine, une maîtresse stagiaire qui était avec elle, lui a dit que c’était possible. Alors elle l’a fait !
Comme nous avons fait des graphiques des températures que nous relevons deux fois par jour les jours d’école, nous avons comparé les graphiques d’Emi à nos graphiques de température.
Nous avons découvert que les graphiques d’Emi nous donnaient des informations qu’on n’y avait pas mises : par exemple, on peut lire combien de francs valent 3,50 €.Alors que les graphiques de température n’indiquent que les informations que nous y avons mises. La maitresse a dit que ça s’appelait une « fonction linéaire », et que ça sert a représenter des relations de proportionnalité.
Emi a décidé de faire un graphique encore plus grand, pour qu’il aille jusqu’à au moins 200 francs, et qu’il soit plus utile… à suivre !
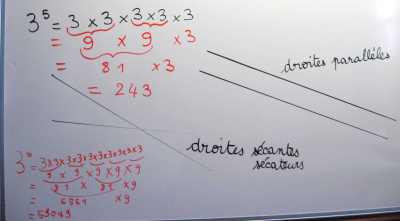
Combien de diagonales a un polygone ?
Un jour, Lewis a présenté un drôle de polygone à 20 côtés.
Valentine et Mélanie ont cherché à savoir combien ce polygone avait de diagonales.
Mais ce n’était pas un problème facile à résoudre !
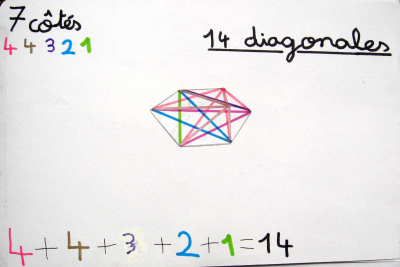
Pour cela, elles ont commencé par tracer des polygones méthodiquement, et à en compter le nombre de diagonales après les avoir tracées.
On a remarqué qu’elles ont inventé une technique pour ne pas en oublier : elles ont tracé d’une même couleur toutes les diagonales qui partent d’un même sommet.
À ce moment-là, cela devenait difficile de continuer avec des polygones irréguliers. Quelques élèves de CM2 ont continué cette recherche avec des polygones réguliers, en cherchant une règle qui leur éviterait de construire des polygones de 20 côtés : les risques d’erreurs devenaient trop importants.
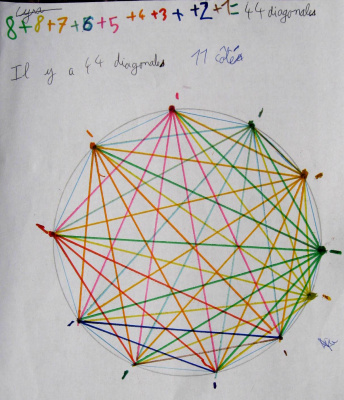
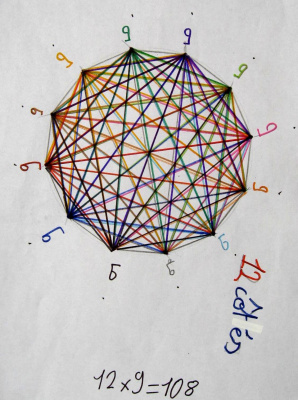
Voici le travail de Lysa et d’Élia pour 11 et 12 côtés :
Le groupe des CM2 a cherché la règle ensemble, mais c’était difficile :
ils ont présenté leurs difficultés à la classe, et la recherche s’est terminée avec l’aide de la maitresse :
Puis on a appliqué la formule pour parvenir à la réponse du problème initial :
un polygone de 20 côtés a 170 diagonales.
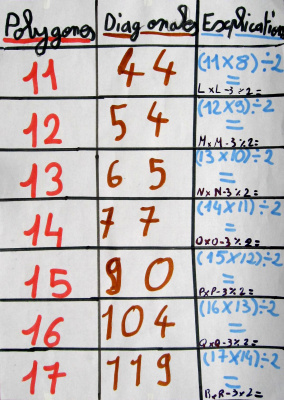
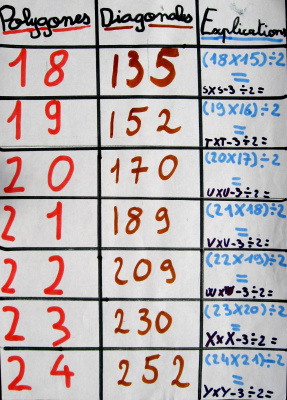
Mais Valentine et Mélanie, aidées par Sullivan, voulaient explorer la formidable formule qui permettait de calculer le nombre de diagonales de n’importe quel polygone…
Pour cela, il leur fallait un grand tableau pour calculer…
un polygone à 100 000 côtés, combien a-t-il de diagonales ?
Et oui, la réponse est : 4 milliards 999 millions 850 mille. Presque 5 milliards !
Pour trouver le milieu…
Voici une recherche menée à partir d’une idée découverte par Bosley : une technique pour trouver vite le milieu entre deux nombres.
Voici l’exemple choisi par Bosley pour nous présenter sa trouvaille :
Chaque élève a vérifié que la formule proposée par Bosley fonctionnait pour un exemple.
À la fin, les élèves ont réalisé des affiches de quelques exemples de la découverte, pour les afficher en classe et ainsi les conserver sous les yeux.
Voici les exemples mis au propre :
Les élèves ont ensuite voulu traduire cette technique en « formule » à la manière de la maitresse, qui s’en sert pour mieux traduire en langage mathématique les idées proposées par les élèves, avec des lettres pour désigner les nombres qu’on connait, et d’autres lettres pour désigner les nombres qu’on cherche.
Mais la recherche n’est pas terminée : n’y aurait-il pas une manière encore plus rapide de trouver le milieu entre deux nombres ?